[CS] TIL 13. 재귀, 병합정렬
- 함수를 재귀적으로 사용하는 코드를 작성할 수 있어야 한다.
- 재귀를 활용한 병합 정렬을 구현할 수 있어야 한다.
boostcourse의 모두를 위한 컴퓨터 과학 (CS50 2019) 강의를 듣고 정리한 필기입니다. 😀
1. 재귀(Recursion)
버블 정렬과 선택정렬의 big-O는 O(n²)이다. 우리는 아직 살펴보지 않은 수많은 정렬알고리즘 중에서 이것보다 더 나은 것이 있는지를 살펴볼 것이다. 그러기 위해서는 먼저 배워야 할 개념이 있다.
알고리즘을 구현하는 코드를 작성하다 보면 동일한 작업을 반복해야 할 때나, for문을 활용해서 같은 루프를 돌 때가 있다. 이럴 때 사용하는 것이 재귀(Recursion)이다. 재귀란 어떤 함수가 스스로 호출하는 것을 말한다.
1.1 전화번호부 알고리즘
이것을 이해하기 위해선 TIL2에서 배웠던 전화번호 찾기를 생각해보자. 우리는 전화번호부에서 Mike Smith를 찾고 있었다. 아래 그림을 봐도 알겠지만, 나는 이때 반복문을 강조하면서 배웠다.
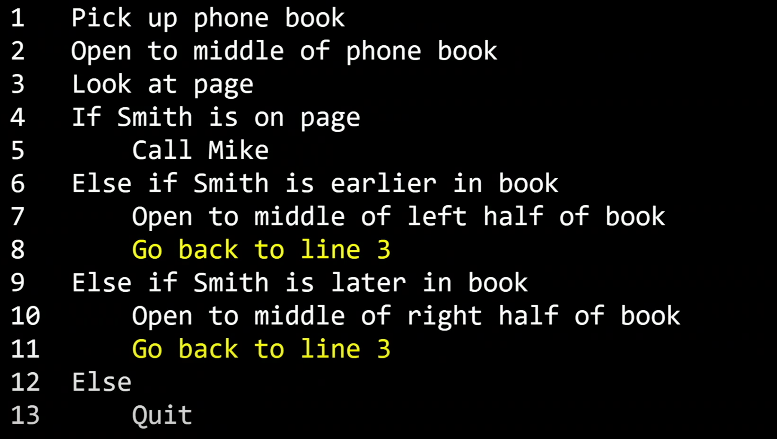
이런 반복문을 없애면 더 빠르고 간결하게 풀 수 있는지 보자. 7번째 줄은 책의 왼쪽 가운데를 펼치고, 10번째 줄에서는 오른쪽 가운데를 펼쳐보라고 한다. 이렇게 왼쪽이나 오른쪽 가운데를 확인하는 이유는 오른쪽이나 왼쪽의 남은 절반에서 찾다 보면 찾는 범위를 좁혀지기 때문이다.
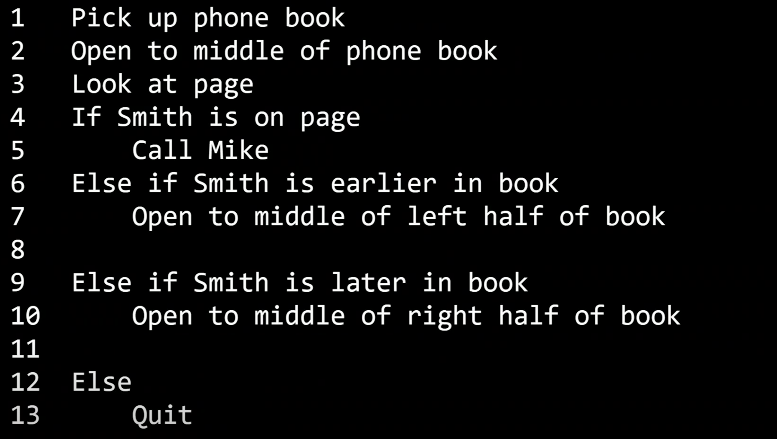
알고리즘도 이와 동일하다. 위 수도코드를 보자. 복잡하게 책을 펴고, 오른쪽을 보고, 혹은 왼쪽을 보고, 3번째 줄로 돌아가고 등등…. 이렇게 복잡하게 여기저기 이동하면서 이것저것을 다시 하지 말고, 직관적으로 책의 왼편을 탐색하거나 오른편을 탐색하라고 했다. 특정 줄로 가라고 할 필요 없이 무엇을 할지만을 알려주면 되는 것이다.
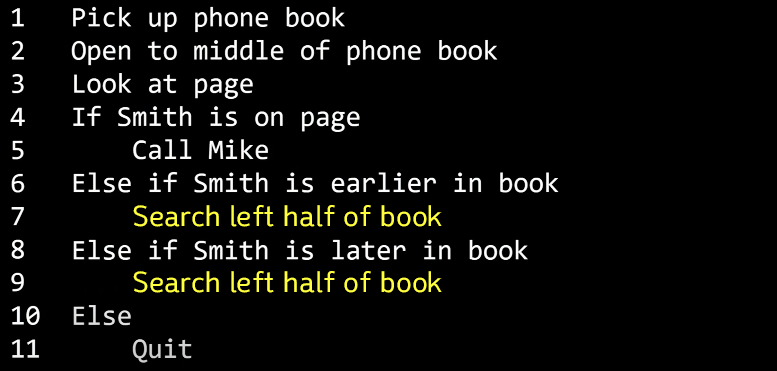
노란색으로 표시된 두 줄을 보면 단순 순환논리처럼 보일 수도 있다. Mike Smith를 어떻게 찾을지 물으면 그냥 Mike Smith를 찾으라는 것과 같아 보인다. 여기서 중요한 점은 같은 것을 단순히 반복(3번째 줄로 돌아가서 반복해라)이 아니라 문제의 크기를 절반에서 절반으로, 또 절반으로 줄여나간다는 것이다. 이것이 재귀의 기본 예시이다. 우리의 프로그램이나 알고리즘을 계속, 스스로가 호출하는 것이다. 위의 코드는 Search라는 함수이다.
1.2 마리오 벽돌 알고리즘

우리는 이제 중첩루프에서 보았던 마리오 게임의 벽돌을 만드는 알고리즘을 살필 것이다. TIL5에서 만든 N×N 블럭이 아니라 위의 그림처럼 계단 형식의 벽돌블럭을 쌓을 것이다.
#include <cs50.h>
#include <stdio.h>
void draw(int h);
int main(void)
{
int height = get_int("Height : ");
draw(height);
}
void draw(int h)
{
for (i = 1; i <= h; i++)
{
for (j = 1; j <= i; j++)
{
printf("#");
}
printf("\n");
}
}
위 코드를 찬찬히 읽어보면 height에 사용자에게 입력받은 계단의 크기를 할당하고, draw()라는 함수를 이용해서 사용자가 원하는 높이의 계단을 그린다. draw() 함수에서는 i는 행을 뜻하고 j는 열을 뜻한다. 높이를 입력받아야 하기 때문에 i와 j에 대한 for문을 중첩하여 계단을 그려준다.
우리가 이 프로그램에서 주의 깊게 봐야 할 곳은 반복되는 구간이다. 어디가 반복될까? draw()함수가 반복되는 것을 볼 수 있다. 4단짜리 계단을 놓고 생각해보면 높이 4의 계단은 높이 3의 계단에서 한 줄이 추가된 것이고, 높이 3의 계단은 높이 2의 계단에서 한 줄이 추가된 것이다. 높이 2의 계단도 마찬가지일 것이다. 이렇게 높이 n의 계단은 높이 n-1의 계단에 한 단을 추가하는 행위를 반복하는 걸 알 수 있다. 100단이든 1,000단이든 동일할 것이다. 물론 높이 0의 계단은 추가할 것도, 추가해야 할 곳도 없다. 자 이제 이것을 재귀적으로 호출하도록 만들어보자.
void draw(int h)
{
draw(h-1);
}
처음 고민할 것은 높이 4에 해당하는 계단을 만들기 위해서 우리는 무엇을 해야하는가 이다. 우리는 아마도 3단의 계단을 만들어야 할 것이다. 해서 우리는 draw(h-1);를 draw() 함수 안에 적어주었다. 이것이 끝일까? 여기서 끝이 난다면 draw()함수는 끝임없이 자기 자신을 호출하면서 빼기만할 것이다. 따라서 우리에게는 멈춰야할 시점이 필요하다.
void draw(int h)
{
if (h == 0)
{
return;
}
draw(h-1);
}
위에도 말했듯이 높이가 0이라면 계단을 그릴 필요가 없다. 때문에, h가 0이 될 때까지. draw(h-1);를 실행 시켜 더욱더 깊게 들어가면 된다.
void draw(int h)
{
if (h == 0)
{
return;
}
draw(h-1);
for (int i = 0; i < h; i++)
{
printf("#");
}
printf("\n");
}
h가 0이 되어 맨 첫줄에 있는 조건문이 수행된다면 어떻게 될까? ` return 같에 의해서 h가 1일 때의 draw(h-1);줄로 다시 나오게 된이다.(1에서 1을 빼기 전으로 다시 돌아왔다고 보면 된다.) 그러면 컴퓨터는 draw(h-1); 다음 줄에 있는 코드를 실행하게 될 것이다. for 문을 통해 #를 하나 그리고 나면 코드가 끝이 난다. 그러면 다시 h가 2일 때의 draw(h-1);` 줄로 나오게 된다. 이것을 끊임없이 반복하다 보면 아래와 같은 결과물을 볼 수 있다.
#
##
###
####
...
재귀적으로 작성됨 draw()를 코드에 붙이면 아래처럼 완성된다. 이렇게 재귀를 사용하면 중첩 루프를 사용하지 않고도 하나의 함수로 동일한 작업을 수행할 수 있다.
#include <cs50.h>
#include <stdio.h>
void draw(int h);
int main(void)
{
int height = get_int("Height: ");
draw(height);
}
void draw(int h)
{
// 높이가 0이라면 (그릴 필요가 없다면)
if (h == 0)
{
return;
}
// 높이가 h-1인 피라미드 그리기
draw(h - 1);
// 피라미드에서 폭이 h인 한 층 그리기
for (int i = 0; i < h; i++)
{
printf("#");
}
printf("\n");
}
2. 병합정렬

지난 시간까지 배원 정렬방법은 두가지 이다. 하지만 우리가 아직 공부하지 않은 대표적인 정렬방법이있다. 그것은 바로 병합정렬이라는 것인데, 버블정렬이나 선택정렬보다도 뛰어난 알고리즘으로 널리 알려져있다. Big-O표기법만 확인해도 병합정렬은 O(n log n)으로 O(n²)보다 훨씬 빠르다는 것을 알고 있다. 이러한 병합정렬의 방법은 탐색해야할 데이터의 요소가 한 개가 될 때까지 계속 반으로 나누다가 크기를 비교하며 다시 합쳐나가는 정렬방법이다. 이것은 전화번호부의 분할 정복 탐색처럼 데이터를 반으로 나누어간다는 공통점이 존재하며, 병합 정렬되는 과정이 재귀적으로 구현되된다는 특징을 가지고 있다. 이러한 병합정렬의 정의를 의사코드로 나타내면 다음과 같다.
On input of n elements
If only one item
Return
Else
sort left half of elements
sort right half or elements
merge sorted halves
왜 요소가 한 개가 될 때까지 계속 반으로 나누는 걸까? 이것은 요소가 하나라면 이미 정렬된 거나 다름없기 때문이다. 의사코드만으로 완전한 이해가 어려우니 아래 그림을 같이 보겠다.
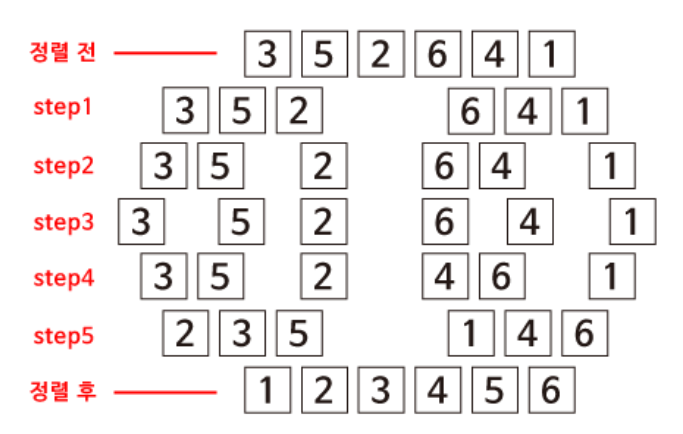
① 차근차근 하나하나 살펴보면 우리는 최초에 정렬되지 않은 숫자들을 가지고 있다.
3 5 2 6 4 1
② 이것들을 반으로 나눈다.
| 3 5 2 | 6 4 1 |
③ 그리고 나눠진 부분 중 첫번째를 한번 더 반으로 나눈다.
| **3 5 | 2** | 6 4 1 |
④ 주어진 요소들(왼쪽, 오른쪽 모두) 모두가 하나가 될 때까지 나눈다.
| **3 | 5** | 2 | 6 4 1 |
⑤ 이 숫자가 오른쪽, 왼쪽 각각 하나씩 남았으니, 더 이상 나누지 않고 두 숫자를 다시 병합한다. 단, 이때 작은 숫자가 먼저오도록 한다. 5보다 3이 더 작음으로 자리는 바꾸지 않는다.
| 3 5 | 2 | 6 4 1 |
| ⑥ 이제 3 5 와 2, 이 두 개의 부분을 병합한다. 각, 부분들의 숫자들을 앞에서부터 순서대로 읽어들여 비교하여 더 작은 숫자를 병합되는 부분 앞으로 가지고 온다. 즉, 우리에게 [ 4 7 | 2 5 ] 가 있다면 4와 2를 먼저 비교해서 2를 가지고 온다. 그 후 4와 5를 비교해서 4를 가지고 온다. 또, 7과 5를 비교해서 5를 가지고 오고, 남은 7을 마지막에 배치하면 된다. |
| 2 3 5 | 6 4 1 |
⑦ 6 4 1 부분도 2 3 5 부분과 똑같은 과정을 거친다.
| 2 3 5 | 1 4 6 |
⑧ 마지막으로 각각 정렬된 왼쪽 3개와 오른쪽 2개의 두 부분을 병합한다.
2와 1을 비교하고, 1을 가져옵니다. 2와 4을 비교하고, 2를 가져온다. 여기서 오른쪽에 있는 숫자를 맞는 자리에 배치를 시켰으니 2 다음 수인 3을 비교한다. 3과 4를 비교하고 3을 가지고 온다. 역시나 오른쪽에 있는 숫자 3을 맞는 자리에 배치 시켰을 때문에 3 다음 수인 5와 4를 다시 비교한다. 4를 가지고온 다음, 5와 6을 비교해 5를 가지고 온다. 이제 마지막 숫자인 6만 남았기 때문에 5 다음 자리에 6을 가지고 오면 된다.
1 2 3 4 5 6
전체 과정을 요약해서 도식화해보면 아래와 같다.

이러한 방법을 ‘병합 정렬’ 이라고 한다. 이러한 병합 정렬의 실행시간은 얼마일까? 무엇인가를 계속해서 절반으로 나눌 때 이 과정을 설명하는 수식이나 함수가 바로 로그(log)이다. 알고리즘을 얘기할 때 무언가 절반으로 계속 나눈다면 로그함수로 표현할 수 있다. 만약 크기 6인 배열을 쪼개서 크기 1인 배열 6개로만드는데 필요한 과정은 밑이 1.817…인 로그이다. 배열의 크기는 매번 다르기 때문에 log n으로 표기 될 것이다.

위 그림의 높이가 log n에 해당한다. 그리고 병합정렬의 실행 시간의 상한(Big-O)는 O(n log n) 가 된다. 숫자들을 반으로 나누는 데는 O(log n)의 시간이 들고, 각 반으로 나눈 부분들을 다시 정렬해서 병합하는 데 각각 O(n)의 시간이 걸리기 때문이다. 실행 시간의 하한도 역시 Ω(n log n) 이다. 숫자들이 이미 정렬되었는지 여부에 관계 없이 나누고 병합하는 과정이 필요하기 때문이다.
